Description
Forecasts time series with seasonality with an additive model. The ETS function stands for Triple Exponential Smoothing and is a statistical algorithm for time series forecasting based on the Holt-Winters model. The ETS is a way to model three aspects of the time series: its average, its trend, and its seasonality.
There are two versions of the model, one being additive and used on most time series, and the other one being multiplicative, more adapted to exponential trends. Pigment chose to use the additive model.
Syntax
FORECAST_ETS(Input Block, Seasonality_length [, Ranking Dimension] [, Alpha] [, Beta] [, Gamma])
Input Blockis the data source on which the ETS forecast is computed, and must be metric with data points as an expression of Integer or number type. The metric must be defined at least on theRanking DimensionDimensionSeasonality_lengthis the length seasonality of theInput Block, expected as an integer. ex: if you observe a quarterly on a metric defined by month, the Seasonality length is 3; if you observe a yearly seasonality on a metric defined by month, the Seasonality length is 12.Ranking Dimensionis a dimension applied to the time series taken in theInput Block. It is optional if it is a datetime dimension from the calendar, but mandatory if it is not or if the metric is defined on several time dimensions.Alphadata smoothing factor, with a value between 0 and 1. The default value is 0.25. It is optional but mandatory in case beta and gamma are precisedBetatrend smoothing factor, with a value between 0 and 1. The default value is 0.1. It is optional but mandatory in case alpha and gamma are precisedGammaseasonal change smoothing factor, with a value between 0 and 1. The default value is 0.25. It is optional but mandatory in case alpha and beta are precised
All last 4 parameters are optional. If one of the last 3 parameters is filled, all the other optional parameters must be filled too.
Note: The Input Block number of data points must be at least twice the seasonality for the ETS function to have the desired behavior. This means that for a time series with a 1-year seasonality, at least 2 years of data.
Your dataset can contain a number of data points not equal to a round multiple of the seasonality, meaning for a yearly seasonality, you don’t need to have exactly 2 or 2 years of data points, it can also be 2.5 years (as long as it is higher than 2 years).
Return type
All the time series cells will be filled by an integer or decimal value starting from the first empty cell until the last value of the datetime dimension (ranked chronologically).
Note: the current implementation of the ETS function does not optimize missing data points in the time series: it is recommended to input plausible values in the empty cells.
Example
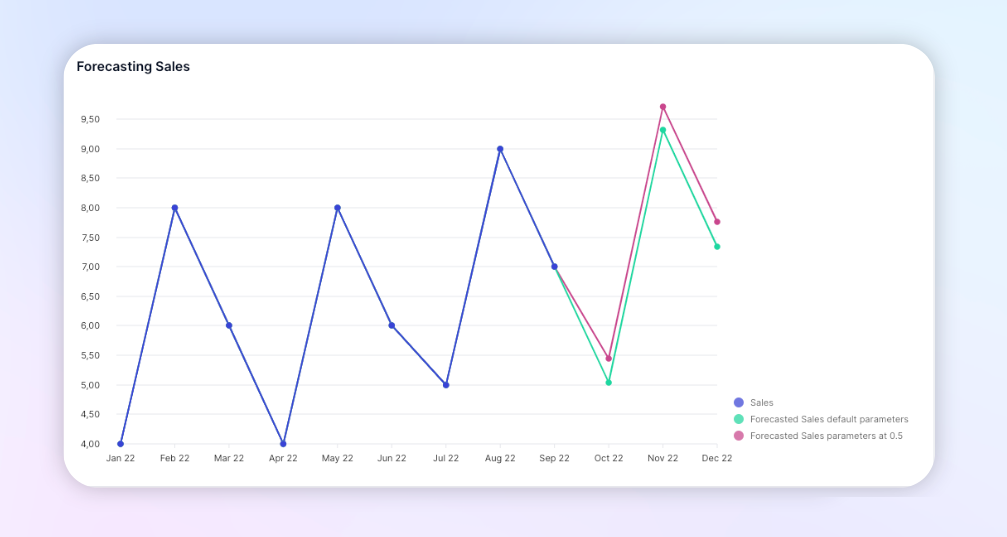
Metric Sales defined on 1 Dimension, with a 3-month seasonality
| Month | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sales | 4 | 8 | 6 | 4 | 8 | 6 | 5 | 9 | 7 |
Forecasted Sales default parameters =FORECAST_ETS('Sales',3,'Month')
Forecasted Sales parameters at 0.5 =FORECAST_ETS('Sales',3,'Month',0.5,0.5,0.5)
Note: The Input Block can have empty values at the beginning of the series: this won’t impact the result of the ETS forecasting, as long as at least 2 times the seasonality in terms of datapoint is non empty.
Documentation
https://www.sciencedirect.com/science/article/abs/pii/S0169207003001134?via%3Dihub






